FIG. 1: Cut-off = 400 µg/L 

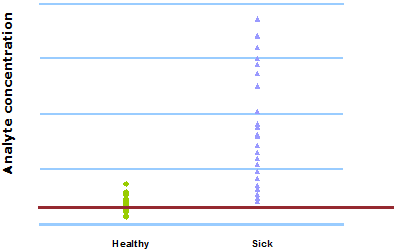
FIG. 2: Cut-off = 500 µg/L

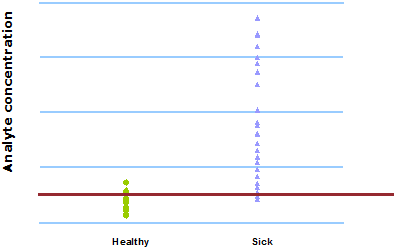
However, sometimes you have to apply different cut-offs to different patient groups. An example: we want to use a new parameter to differentiate patients who are infected from those who are not infected.

We try to find a suitable cut-off but as can be seen in Fig. 3, there is no ideal cut-off due to overlap of the ranges of results from the infected and the non-infected group.

FIG. 3: Same cut-off for all patients

But in this case the parameter tested is not only an infection marker but also an acute-phase reactant. This means that surgery will increase the level, also without an infection.

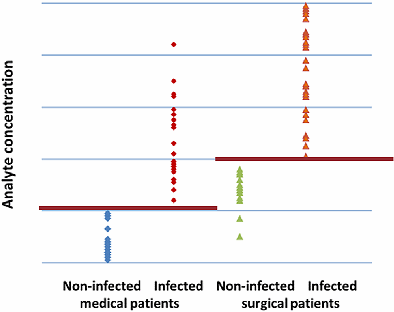
Let us try instead to divide the patients into medical and surgical subgroups and further divide these subgroups into infected and non-infected.

Now, as can be seen in Fig. 4, we are able to define separate cut-offs for the medical and the surgical groups, respectively. Now the parameter seems to be useful in the differentiation of infected from non-infected patients.

FIG. 4: Patient-group-specific cut-offs

It should always be kept in mind that a cut-off has to be chosen based on one population and tested on another population. A reason for this is that a data-driven choice of cut-off often boosts the diagnostic performance of a biomarker.

STUDY POPULATION

PREDICTIVE VALUES

The predictive value of a test is a measure in percentage of the times that the value (positive or negative) is the true value, i.e. the percent of all with a positive test who are actually sick is the positive predictive value (PPV) and the percent of all with a negative tests who are not sick is the negative predictive value (NPV).

TABLE I: Comparing a method with the "truth"

		Disease (the “truth”)		Predictive values
		+	-
Test	+	True positives (TP)	False positives (FP)	PPV = TP / (TP + FP)
	-	False negatives (FN)	True negatives (TN)	NPV = TN / (TN + FN)
		Sensitivity = TP / (TP + FN)	Specificity = TN / (TN + FP)	Prevalence= (TP + FN) / (TP + FN + TN + FP)

As can be seen in Table I the sensitivity, which determines the number of true positives, and the specificity, which determines the number of true negatives, both have a strong impact on the predictive values.

However, the prevalence, i.e. the fraction of sick persons in the population tested, also has a strong impact on the predictive values of a test.

INFLUENCE OF PREVALENCE ON PREDICTIVE VALUES

As can be seen in Fig. 5 PPV increases with increasing disease prevalence, whereas NPV decreases with increasing disease prevalence. To understand why that is, consider a situation where everyone in a population is sick (prevalence = 100 %).

In this situation, every positive result would be a true positive and there are no false positive results. Then the PPV would be 100 %. Conversely, if no one in the population is sick (prevalence = 0 %), every positive result would be a false positive.

As there are no true positives, the PPV is 0 %. Thus we can see that the disease prevalence influences the PPV by influencing the true positive and false positive rates.

Similar arguments can be used for NPV. When there are only sick persons in a population, every negative result would be false negative, and if there are only healthy persons in a population, every negative result would be true negative.

FIG. 5: Predictive values as function of prevalence. Assay sensitivity = 90 % and assay specificity = 90 %

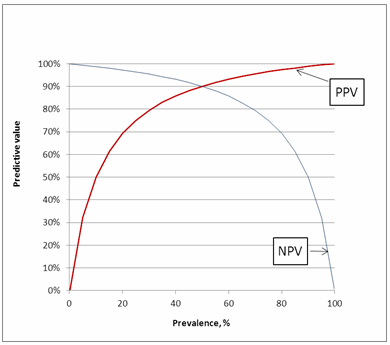
So what do predictive values versus prevalence tell us?

We can choose prevalence; say 10 %. It means that with 100 persons in the study, we have 10 who are sick and 90 who are healthy.

If the assay has sensitivity 90 %, then 9 of the sick persons (90 % of 10 persons) will get a true positive test and one (10 – 9) will get a false negative test. If the assay has specificity 90 %, then 81 of the healthy persons (90 % of 90 persons) will get a true negative test and 9 will get a false positive test.

The results are illustrated in Fig. 6.

FIG. 6: Test results Results of sick persons are colored red, results of healthy persons are colored blue. Positive test result shown as +, negative test result as ¸.

When we look at Fig. 6, we can see who is sick and who is healthy because they have different colors. However, when we get a test result, we are “color blind” and only see whether it is positive or negative like in Fig. 7.

FIG. 7: Test results Positive test result shown as +, negative test result as ¸.

We have 18 + and 82 ÷. From the calculations above we know that only 9 of the 18 + are sick and only 81 of the 82 ÷ are healthy. From this information we can calculate the predictive values:

PPV = 100 % × 9/18 = 50 %

NPV = 100 % × 81/82 = 99 %

A positive predictive value of 50 % means that in half of the cases where we get a positive result the person is sick and in half of the cases the person is healthy. Similarly, a negative predictive value of 99 % means that when we get a negative result, the patient is in 99 % of the cases healthy and only in 1 % of the cases the person is sick.

These predictive values we can easily find directly when we use Fig. 8.

FIG. 8: Predictive values as function of prevalence 
 

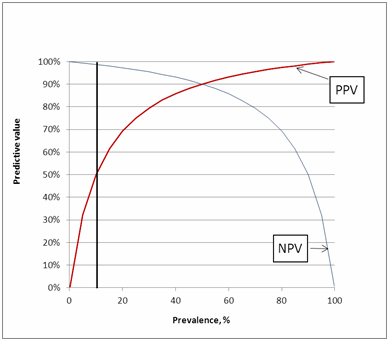
So what Fig. 5 and Fig. 8 show us is that it is important to remember that the predictive values are not universal but depend on each specific clinical setting.

INFLUENCE OF SENSITIVITY AND SPECIFICITY ON PREDICTIVE VALUES

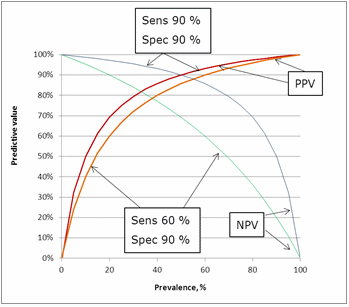
The influence of sensitivity can be seen in Fig. 9. Lowering the sensitivity from 90 % to 60 % has an impact on the predictive values. The greatest impact is on the negative predictive value because lowering the sensitivity means increasing the number of false negatives.

  

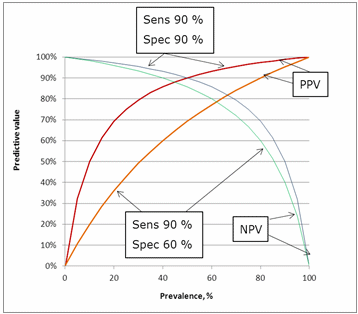
The influence of specificity can be seen in Fig. 10. Lowering the specificity from 90 % to 60 % has an impact on the predictive values. The greatest impact is on the positive predictive value because lowering the specificity means increasing the number of false positives.

FIG. 10: Influence of specificity on the predictive values
  

INFLUENCE OF TOTAL NUMBER OF PATIENTS IN A STUDY

The CLSI EP12-A2 guideline [6] recommends that as a minimum testing should continue until results from at least 50 positive specimens are obtained and that at least 50 negative specimens using the comparative method should be obtained to determine the specificity of the candidate method.

We can make a table like Table I where a method is compared to the “truth” and calculate the sensitivity and the specificity with the 95 % confidence intervals and use it to see an example of the influence of the number of patients included in a study.

TABLE II: Sensitivity and specificity confidence intervals, n = 145

n = 145		Disease (the “truth”)		Sensitivity, % (95 % CI)	Specificity, % (95 % CI)
		+	-
Test	+	30	12	90.9 (77.4 – 97.5)	89.3 (85.3 – 91.2)
	-	3	100

TABLE III: Sensitivity and specificity confidence intervals, n = 1450

n = 1450		Disease (the “truth”)		Sensitivity, % (95 % CI)	Specificity, % (95 % CI)
		+	+
Test	+	300	120	90.9 (87.4 – 93.5)	89.3 (88.3 – 90.0)
	-	30	1000

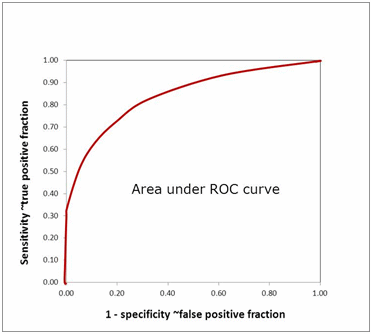
AREA UNDER ROC CURVE

The CLSI EP812-A2 guideline [6] mentions that an appropriate measure to describe diagnostic accuracy includes ROC curves.

An ROC curve shows the relationship between clinical sensitivity and specificity for every possible cut-off. The ROC curve is a graph with:

• The x-axis showing 1 – specificity (= false positive fraction = FP/(FP+TN))
• The y-axis showing sensitivity (= true positive fraction = TP/(TP+FN))

Thus every point on the ROC curve represents a chosen cut-off even though you cannot see this cut-off on the graph. What you can see is the true positive fraction and the false positive fraction that you will get when you choose this cut-off.

The area under the ROC curve (AUROC) of a test is often used as a criterion to measure the test's discriminative ability, i.e. how good is the test in a given clinical situation. The closer an ROC curve is to the upper left corner, the more efficient is the test and the closer to 1.0 the AUROC will be.

FIG. 11: Area under ROC curve 
 

AUROC is also often used in comparisons between biomarkers. The advantage of using AUROC to compare biomarkers is that the AUROC reveals real differences in diagnostic performance and not just differences in sensitivity and specificity due to different choices of cut-off.

When comparing AUROCs, confidence intervals need to be taken into consideration. The confidence interval of the difference between two AUROCs is determined by numbers of healthy and sick participants in the study and whether or not the two AUROCs were obtained on the same specimens or different specimens. If a confidence interval for the difference between AUROCs contains the value 0.0, then the two AUROCs do not differ significantly.

TABLE IV: Comparing AUROC; 50 healthy, 20 sick in all studies

	AUROC 1	AUROC 2	Difference (95 % CI)
Same specimens	0.90	0.81	0.09 (-0.005 – 0.185)
Different studies/ specimens	0.90	0.74	0.16 (-0.007 – 0.327)

In Table IV we can see that if we have a small study with 50 healthy persons and 20 sick persons and we compare two biomarkers using the same specimens, then biomarker 1 with AUROC 0.90 and biomarker 2 with AUROC 0.81 cannot be claimed to be significantly different from a diagnostic point of view (under the specified circumstances of the study). If biomarker 2 had had AUROC 0.80, they would have been claimed significantly different.

In Table IV we can also see that if we have two small studies, each having 50 healthy persons and 20 sick persons and we compare two biomarkers, then biomarker 1 (study 1) with AUROC 0.90 and biomarker 2 (study 2) with AUROC 0.74 cannot be claimed to be significantly different from a diagnostic point of view (under the specified circumstances of the studies).

If biomarker 2 had had AUROC 0.73, they would have been claimed significantly different. In addition it can also always be discussed whether the two studies had groups with a similar spectrum of disease.

Thus it can be seen that when we have two separate studies, the difference between two areas under ROC curves will be greater before it is considered significant compared to the situation where we look at a difference between two ROC curves based on the same samples in the same study.

FIG. 12: Comparing area under ROC curve (hypothetical)
   

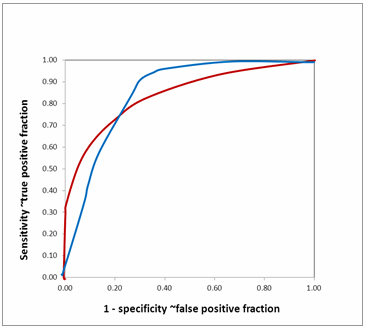
Equal AUROCs for two biomarkers show that their overall performances are similar. However, it does not mean that both the curves are identical. They may cross each other as in Fig. 12. The two ROC curves have nearly identical AUROC.

However, they cross each other. The biomarker with the red curve performs better than the biomarker with the blue curve when high specificity (low false positive fraction) is needed, while the biomarker with the blue curve performs better than the biomarker with the red curve when high sensitivity is needed.

It is justified to look at partial areas under ROC curves in such situations where AUROCs are nearly identical but differ in their diagnostic efficacy in specific segments.

If the biomarkers you are comparing are markers of a disease with a grave prognosis, you would want to have high specificity. Thus you would choose the biomarker with the red curve.

However, if the biomarkers you are comparing are used to select patients who need to undergo a confirmatory test for a disease that is important to treat, then you would choose the biomarker with the blue curve to have high sensitivity.

ROC curves with different total AUROCs may be similar in specific regions. In such cases it is also an advantage to look at partial AUROC.

THE INFLUENCE ON DIAGNOSTIC PERFORMANCE

We now know that:

• Cut-off has an influence on diagnostic performance
• Cut-offs can be dependent on subgroups (comorbidities)
• Spectrum of disease has an influence
• Predictive values are highly dependent on
  • Prevalence
  • Sensitivity
  • Specificity
• Number of participants in a study has a great influence on the confidence interval for diagnostic performance measures
• When differences between AUROCs are compared, confidence intervals are important
• Partial AUROC analysis should be used when relevant
• To claim usefulness of a biomarker in diagnosis the study population has to be the intended-use population