Printed from acutecaretesting.org
October 2009
Diagnostic accuracy – Part 2
Predictive value and likelihood ratio
PREDICTIVE VALUES
As pointed out previously, sensitivity and specificity define the discriminative power of a diagnostic procedure (test) and give us the proportion of diseased and healthy individuals identified correctly by the test, respectively.
However, sensitivity and specificity tell us nothing about the predictive abilities of a positive or a negative result.
What a physician wants most from any diagnostic procedure is the answer to the following questions:
"If a person has a positive test result, how sure can I be that this person has the disease? If a person has a negative test result, how sure can I be that this person does not have the disease?"
Very useful measures of diagnostic accuracy, which give answer to these questions, are predictive values: positive predictive value (PPV) and negative predictive value (NPV).
Positive predictive value (%) defines the probability of the disease in a person who has a positive test result. It represents the proportion of the diseased subjects with a positive test results (TP, true positives) in a total group of subjects with positive test results (TP/(TP+FP)).
Therefore, positive predictive value relates to the predictive ability of a test to identify disease in individuals with positive results.
Negative predictive value (%) defines the probability of the absence of the disease in a person who has a negative test result. It indicates the proportion of healthy subjects with negative test results (TN, true negatives) in a total group of subjects with negative test results (TN/(TN+FN)).
Therefore, negative predictive value relates to the predictive ability of a test to identify the absence of the disease in individuals with negative test results.
In Part 1 of this article (June 2009) we evaluated the sensitivity and specificity of S-100B, a new potential marker for acute ischemic stroke. Let us now imagine that we want to calculate predictive values, the PPV and NPV, for S-100B in acute ischemic stroke.
Again, the first step in calculating measures of diagnostic accuracy is to make a 2 × 2 table with groups of subjects divided according to a gold standard or reference method (diagnostic criteria) in columns and categories according to test (S-100B) result in rows (TABLE 1).
TABLE 1: 2 × 2 table for calculating measures of diagnostic accuracy
|
individuals |
individuals |
|
| S-100B > 0.5 µg/L |
TP (N = 90) |
FP (N = 40) |
| S-100B < 0.5 µg/L |
FN (N = 10) |
TN (N = 60) |
Using formulas for predictive values previously stated in this text we can calculate PPV and NPV. At a cut-off value of 0.5 µg/L for serum S-100B protein, PPV is 69.2 % and NPV is 85.7 %. How do we interpret those figures?
PPV of 69.2 % means that 69 out of 100 individuals with positive test results actually have the disease. So, the greater the PPV, the more convincing is the positive result.
In other words, if an individual presenting with stroke symptoms at the emergency department of our neurology clinic has an elevated value of S-100B protein (> 0.5 µg/L), and given the fact that a PPV for that marker is 69.2 %, the physician knows that there is a 69.2 % probability that this person has a stroke.
What does NPV tells us? An NPV of 85.7 % means that if we test a group of individuals with stroke symptoms and 100 of them have a negative result of the test, disease is actually absent only in 85 out of those 100 individuals with negative test results.
The remaining 15 individuals who have negative test results actually have a disease and are so-called false negatives. Those individuals are missed by the test. The higher the NPV, more conclusive is the negative result.
So, if a subject has an NPV of 85.7 %, a physician knows that that there is a 85.7 % probability that this person does not have a stroke.
It was already previously mentioned that some measures of diagnostic accuracy may vary depending on the spectrum of the disease in the studied group as well as on the disease prevalence.
Predictive values are greatly influenced by the prevalence of the disease, meaning that results from one clinical setting cannot be transferred to some other setting with a different prevalence of the disease in the population.
The same marker (S-100B) for the same disease (stroke) must have constant sensitivity and specificity, but predictive values may vary with the ratio of the individuals with the disease in the population under study.
PPV and disease prevalence are positively associated, meaning that PPV is higher in the population with higher prevalence of the disease, whereas NPV is negatively associated with the disease prevalence.
In our theoretical example with a new potential marker for stroke, out of 200 subjects presenting with stroke symptoms there were 100 individuals with stroke and 100 individuals in whom stroke was subsequently excluded.
Hence, the disease prevalence was 50 %. Let us now imagine that the number of healthy individuals increased tenfold. Instead of 100, there are now 1000 healthy subjects. This way, disease prevalence decreases to 9.1 %.
Sensitivity and specificity remain 90 % and 60 %, respectively (TABLE 2). The question is: while specificity and sensitivity remain unchanged, what happens to PPV and NPV as disease prevalence decreases from 50 % to 9.1 %?
TABLE 2: 2 × 2 table for calculating measures of diagnostic accuracy
|
individuals |
individuals |
|
| S-100B > 0.5 µg/L |
TP (N = 90) |
FP (N = 400) |
| S-100B < 0.5 µg/L |
FN (N = 10) |
TN (N = 600) |
PPV is now 18 %, whereas NPV is 98 %. As expected, PPV decreased due to the decrease of the disease prevalence, whereas at the same time NPV increased. A PPV of 18 % means that out of 100 subjects who have positive test results, there will be only 18 who actually have the disease.
The other 72 subjects are false positives.
There are two important things we should remember about predictive values. First, if we test the population with low prevalence of the disease, regardless of the high sensitivity of the test, we will always end up having a high proportion of false positive results due to the low positive predictive value of the test.
That is the reason why tumor markers, for example, perform poorly in screening and confirming cancer in asymptomatic population, in which the prevalence of a malignant disease is low.
Second, since disease prevalence greatly differs depending on the clinical setting and many other characteristics of the population, PPV and NPV from one setting cannot be generalized and used in another clinical setting.
For instance, PPV and NPV obtained in some primary care health institution will differ greatly from a tertiary care university hospital, where disease prevalence may be much higher than in the primary care setting.
That is the reason why some markers, like BNP, perform better in tertiary care institutions than in primary care.
LIKELIHOOD RATIO
Likelihood ratio (LR) is the ratio of two probabilities: (i) probability that a given test result may be expected in a diseased individual and (ii) probability that the same result will occur in a healthy subject.
Likelihood ratio of a positive test (LR+) result is the ratio of the probability that a positive test result is expected in a diseased individual to the probability that a positive result occurs in a healthy subject.
It tells us how many times it is more likely to observe a positive test result in a diseased than in a healthy individual. Likelihood ratio of a positive test can be calculated according to the following formula:
(LR+) = sensitivity / (1 - specificity)
Likelihood ratio of a negative test result (LR-) is the ratio of the probability that a negative test result may be expected in a diseased individual to the probability that a negative result may occur in a healthy subject.
It tells us how many times less likely it is to observe a negative test result in a diseased than in a healthy individual. (LR-) may be calculated according to the formula:
(LR-) = (1 - sensitivity) / specificity
The advantage of likelihood ratios over predictive values is that they are not affected by the changes of the prevalence of the disease and can therefore be used to adopt the results from other investigators to your own patient population.
Moreover, likelihood ratios are very useful measures of diagnostic accuracy, since they have a direct mathematical relationship with pre- and post-test probabilities, allowing us to revise the a priori probability of a disease in a patient by knowing the result of a diagnostic test and its likelihood ratio.
How to revise the a priori probability of a disease in a certain patient?
Pre- and post-test probabilities may be easily revised using a graphical tool called the Fagan nomogram (FIG. 1). By using the Fagan nomogram we can estimate how much the result of a diagnostic test changes the probability that a patient has a disease.
FIGURE 1: Fagan nomogram

To use the Fagan nomogram we need to provide the best estimate of the probability of the disease in an individual, prior to any testing. This probability is usually called the pre-test probability or a priori probability.
The pre-test probability relates to the prevalence of the disease and patient risk factors. We also need to know the result of the test and its likelihood ratio.
If we draw a line connecting the pre-test probability and the likelihood ratio and extend the line until it intersects with the post-test probability axis, then the point of intersection is the post-test probability.
Post-test probability is the updated probability of a disease assigned to a certain patient, using the information of the result of a diagnostic test. If a diagnostic test is of high diagnostic accuracy, it will provide enough information to either greatly increase or decrease the probability of a disease.
If a test has low diagnostic accuracy, it will add no value to the existing probability.
It is generally accepted that (LR+) > 10 aids to rule-in and (LR-) < 0.1 to rule-out. If (LR+) is < 10 or (LR-) > 0.1, the test has little or no value. If LR = 1, the test does not change the disease probability, whatsoever.
Let us see how it works on our example with S-100B, a new potential marker for acute ischemic stroke. (LR+) and (LR-) may be calculated according to the formulas stated previously in the text:
a) (LR+) = sensitivity / (1 - specificity) = 0.90 / (1.00 – 0.60) = 2.25
b) (LR-) = (1 - sensitivity) / specificity = (1.00 – 0.90) / 0.60 = 0.16
Assume that a 74-year-old hypertensive male subject presents to the emergency department with stroke symptoms. Based on the clinical examination the physician estimates a probability of stroke in that patient, prior to any testing, to be as high as 90 %.
An S-100B test is ordered and the result is positive. We draw a line connecting the pre-test probability (90 %) and the likelihood ratio (LR+ = 2.25) and then extend the line until it intersects with the post-test probability axis.
The estimated post-test probability is approximately 97 % (FIG. 2). Since LR+ was low, there was no significant change in the probability. We may conclude that, due to its low diagnostic accuracy for stroke, S-100B was of no use in revising probabilities.
FIGURE 2: Revising probabilities with Fagan nomogram
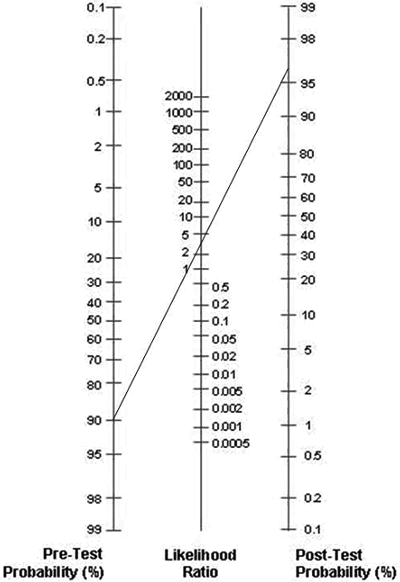
Assume now that the pre-test probability was much lower (60 %) and that S-100B has a (LR+) of 20, instead of 2.25. If we now draw a line connecting the pre-test probability (60 %) and the likelihood ratio (LR+ = 20) and extend the line until it intersects with the post-test probability axis, the estimated post-test probability will again be approximately 97 %.
But this time the change of the pre-test probability of 60 % to the post-test probability of 97 % was significant and we may conclude that S-100B was helpful in revising probabilities.
This was an example of how we can use the information of the result of a diagnostic test and knowledge about the diagnostic accuracy of the test (LR) to update the pre-test probability of a disease in a certain patient.
In the first case with a high probability of stroke, the test did not help much in updating the probability of stroke, since the pre-test probability was high anyway and the test had low added value.
However, in the second case with a lower probability of stroke and a test with better diagnostic accuracy, the updated post-test probability was much higher. The knowledge of the result of the test has significantly changed the estimated probability of a stroke.
To conclude, likelihood ratios are able to assess and combine the complex clinical data and information provided by a diagnostic procedure or a test. Likelihood ratios are highly useful statistics for summarizing diagnostic accuracy, which help clinicians to make important decisions about patient care.
May contain information that is not supported by performance and intended use claims of Radiometer's products. See also Legal info.
Acute care testing handbook
Get the acute care testing handbook
Your practical guide to critical parameters in acute care testing.
Download nowScientific webinars
Check out the list of webinars
Radiometer and acutecaretesting.org present free educational webinars on topics surrounding acute care testing presented by international experts.
Go to webinars